2025年6月26日更新

希薄気体の粘性率は分子運動論から次式で表される³⁾⁴⁾。

　ここに

\( \eta^0 \) ：希薄気体の粘性率

\( M \) ：分子量

\( k_B \) ：ボルツマン定数

\( T \) ：温度

\( \sigma \) ：剛体直径

\( \Omega \) ：衝突積分

衝突積分は、無極性気体に対し、Lennard-Jonesポテンシャルを用いてNeufeldらは次式の経験式を提示している³⁾⁴⁾。

　ここに

\( T^* \) ：無次元温度 [\( T/\left( \varepsilon/k_B \right) \)]

\( \varepsilon \)：特性エネルギ

極性気体に対しては、Stockmayer ポテンシャルを用いてBrokaw は次式を提示している³⁾。

　ここに

\( \delta \)：極牲パラメータ

希薄気体の粘性率は、剛球直径、特性エネルギ、極牲パラメータが分かれば算出できるが、多くの場合これらの物性は、希薄気体の粘性率から逆算されたものであり、極性気体でも式(2.2)を用いているものも多い。また、最近では衝突積分の算出式も物質ごとに異なったものが提案されている。

　\( \delta,\ \varepsilon / k_B,\ \delta \) の例を表2.1に示す。

表2.1 \( \delta,\ \varepsilon / k_B,\ \delta \) の例

	\( \sigma \)[nm]	\( \varepsilon / k_B \)[K]	\( \delta \)
R325)	0.4098	289.65	-
R1256)	0.5235	237.077	-
R143a5)	0.5025	267.1	-
R152a7)	0.463	312	0.62
R1234yf 8)	0.5328	281.14	-

冷媒を含め多くの物質の剛球直径、特性エネルギが報告されている ^{3)4)5)9)10)11)}。しかし、文献によって異なっている場合が多く、剛球直径、特性エネルギは同じ文献のものを用いる必要がある。

　表2.1 および式(1.2) から算出した希薄気体の粘性率を図2.1 に示す。

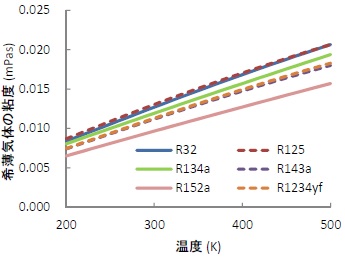
図2.1 希薄気体の粘性率

混合物の希薄気体の粘性率は、次式で近似的に表される³⁾⁴⁾。

　ここに

\( {\eta^0}_m \)：混合物の希薄気体の粘性率

\( y_i \)：組成iのモル分率

\( {\eta^0}_i \)：組成iの希薄気体の粘性率

\( \phi_{ij} \)：相互作用パラメータ

相互作用パラメータはWilke近似法を用いると次式で表される。

　ここに

\( M_i \)：組成iの分子量

式(2.5)から算出した希薄気体の粘性率を図2.2 に示す。

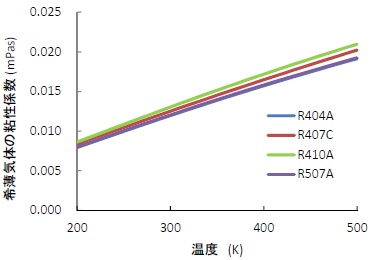
図2.2 混合物の希薄気体の粘性率

ページトップ