粘性率

2025年6月26日更新

粘性率

粘性率は、流動様式を決定付ける物理量で、配管設計には不可欠なものである。粘性率の特徴は温度の上昇、圧力あるいは密度の上昇により粘性率も基本的に上昇するが、凝固点付近の急激な増加、臨界点近傍の増加、さらに低圧領域では圧力あるいは密度の上昇により粘性率が低下する領域があり複雑な挙動を示す。また、圧力を関数にすると等温線に交差が見られるが、密度を関数にすると交差は見られないために、粘性率は温度と密度の関数で提案されている。代表的なものとして希薄気体の粘性率と余剰の粘性率を組み合わせた手法と測定データからパラメータの最適手法を用いて直接相関式を求める手法が知られている。ただし、臨界点近傍の増加は影響範囲が狭く、必要なデータも十分でなく適用されている相関式は少ない。代表的な相関式を冷媒R134aを例として以下に示す。

(1)Huberらの相関式¹⁾

\[ \eta(\rho,T)= \eta ^0 (T)+\Delta \eta = \eta ^0 (T) [1+ B_\eta(T) \rho] +\Delta_H \eta (\rho,T) \]

(1.1)

ここに

\( \eta^0 \) ：希薄気体の粘性率

\( \Delta \eta \) : 密度、温度の関数である剰余粘性率

\( B _ \eta \) : 粘性率の第2ビリアル係数

\( \Delta_H \eta \) : 高次の密度の項

\( T \) : 温度

\( \rho \) : 密度

希薄気体の粘性率\( \eta^0 \) 、第2ビリアル係数\( B_\eta \) 、高次の密度の項\( \Delta_H \eta \) は次式で整理されている。

・希薄気体の粘性率\( \eta^0 \)

\[ \eta ^0 (T) = \frac{0.021357(MT)^{0.5}}{\sigma^2 \vartheta_\eta} \]

(1.2)

ここに

(1.3)

\( \ln(\vartheta_\eta) = \displaystyle \sum_{i=0}^{n} a_i (\ln T ^* ) ^ i \)

(1.4)

\( T^* = k_B T/ \varepsilon \)

\( M \)：分子量

\( T \)：温度

\( \sigma \)：剛球直径

\( a_i \)：係数

\( B \)：ボルツマン定数

\( \varepsilon \)：特性エネルギ

・第2ビリアル係数\( B_\eta \)

\[ B_\eta = N_A \sigma^3 B_\eta ^* \]

(1.5)

ここに

\( N_A \) ：アボガドロ数

(1.6)

\( B_\eta ^* = \displaystyle \sum_{i=0}^{n} b_i ( T ^* ) ^ {t_i} \)

\( b_i, t_i \) ：係数

・高次の密度の項\( \Delta_H \eta \)

\[ \Delta_H\eta=c_1 \rho_r + \left( \frac{c_2}{{T_r}^6} + \frac{c_3}{{T_r}^2} + \frac{c_4}{{T_r}^{0.5}} + c_5 {T_r}^2 \right) {\rho_r}^2 +c_6 {\rho_r}^3 + c_7 \left( \frac{1}{\delta_0-\rho_r}-\frac{1}{\delta_0} \right) \]

(1.7)

ここに

(1.8)

\( \delta_0 = \displaystyle \frac{c_{10}}{1+c_8 T_r + c_9 {T_r}^2} \)

(1.9)

\( T_r = T/T_r \)

(1.10)

\( \rho_r = \rho/\rho_r \)

\( T_c \) ：臨界温度

\( \rho_c \) ：臨界密度

\( c_i \) ：係数

(2)Scalabrin らの相関式²⁾

\[ \eta_r=\sum_{i=1}^{7} n_i {T_r} ^ {g_i} {\rho _r} ^{h_i} +\exp(-2 {\rho_r} ^2) \sum_{8}^{10} n_i {T_r} ^ {g_i} {\rho _r} ^{h_i} \]

(1.11)

ここに

(1.12)

\( \eta_r = \ln (\eta / H_c +1 ) \)

(1.13)

\( H_c= \displaystyle \frac{M^{1/2}{P_c}^{2/3}}{R^{1/6}{N_A}^{1/3}{T_c}^{1/6}} \)

\( P_c \) ：臨界圧力

\( R \) ：ガス定数

\( N_A \) ：アボガドロ定数

\( n_i,g_i,h_i \) ：係数

それぞれの係数については文献を参照のこと。

Huberらの式、およびScalabrinらの式から算出した飽和液、飽和ガスの粘性率を図1.1、両者の偏差を図1.2、温度300Kでのガスの粘性率を図1.3に示す。

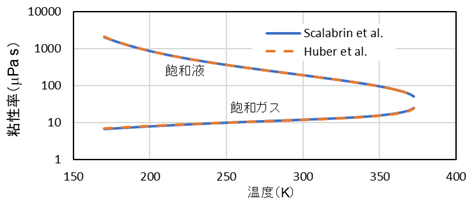
図1.1 R134aの飽和液、ガスの粘性率

図1.2 相関式の偏差

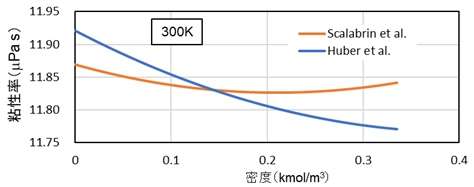
図1.3 R134aのガスの粘性率

　この二式の相関式作成手法は異なるが、主として利用された測定データの多くが同一のものであり、計算値の偏差は小さく測定値のばらつきの範囲にある。粘性率は三重点近傍の高密度域で急激に増加する特徴があり、この特徴を再現するためにHuberらは独立項で、Scalabrinらは対数で対応しており、測定データの再現性に工夫がされている。また、図1.3に見られるように初期密度による粘性率の低下も再現されているが低下割合はHuberらのほうが大きく、300Kでは露点密度まで低下している。ただし、両者の絶対値の差は小さい。一方、R134aのような比較的測定データが充実している場合でも臨界点近傍の粘性率上昇を高精度に再現できるだけのデータは少ない。また、粘性率の測定は毛細管式、円盤式、振動式などがあり、測定の複雑さに加え、系に与える外乱が大きく、熱力学的物性の測定よりばらつきが多い。相関式作成に用いないデータでは数十パーセントの偏差も多くある。

　近年、三重点から超臨界までの幅広い温度、密度に適用できる相関式が提供されるようになってきているが、物質が限られている。粘性率の推算のために、多くの手法が提案されているが、測定値がある場合、状態式と実測値を組み合わせた拡張対応状態原理が比較的信頼性が高いと考えられる。この場合、半理論式のHuberらの式が利用しやすい。冷媒のData BaseのRefprop でも多くの冷媒で利用されている^3,4,5)。

ページトップ