熱交換器のような流体間に温度差がある場合、高温流体から隔板へ熱伝達、隔板内で熱伝導、隔板から低温流体へ熱伝達で熱量が移動する。このような熱伝達と熱伝導による伝熱を統括して熱通過と呼ぶ。

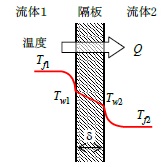
平板の熱通過

　右図のような平板の隔板を介して高温の流体１と低温の流体２間の伝熱を考える。定常状態とすると伝熱熱量Q は一定となり、流体１、２の温度をそれぞれT_f1 、T_f2 、隔板の表面温度をT_w1 、T_w2 、流体１、２の熱伝達率をそれぞれh₁、h₂、隔板の熱伝導率をλ、隔板の厚さをδ、伝熱面積をA とすれば次の関係式を得る。

\[Q=h_1 \cdot \bigl( T_{f1} - T_{w1} \bigr) \cdot A \hspace{10em} (2.1) 　　\]

\[Q=\dfrac{\lambda}{\delta} \cdot \bigl( T_{w1} - T_{w2} \bigr) \cdot A \hspace{10em} (2.2) \]

\[Q=h_2 \cdot \bigl( T_{w2} - T_{f2} \bigr) \cdot A \hspace{10.1em} (2.3) \]

上式より、T_w1 、T_w2 を消去し整理すると次式を得る。

\[Q=K \cdot \bigl( T_{f1} - T_{f2} \bigr) \cdot A \tag{2.4} \]

ここに　

\[K=\dfrac{1}{\dfrac{1}{h_{1}}+\dfrac{\delta}{\lambda}+\dfrac{1}{h_{2}}} \tag{2.5} \]

このK は熱通過率あるいは熱貫流率、K値、U値とも呼ばれ、逆数1/K は全熱抵抗と呼ばれる。

平板が熱伝導率の異なるn層の合成平板から構成されている場合の熱通過率は次式で表される。

\[K=\dfrac{1}{\dfrac{1}{h_{1}}+\sum\limits_{i=1}^n{\dfrac{\delta_i}{\lambda_i}}+\dfrac{1}{h_{2}}} \tag{2.6} \]

 

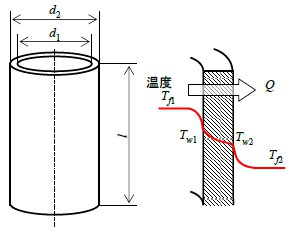
円管の熱通過

　内径d₁、外径d₂の円管内外の高温の流体１と低温の流体２の伝熱を考える。定常状態とすると伝熱熱量Q は一定となり、流体１、２の温度をそれぞれT_f1 、T_f2 、円管の表面温度をT_w1 、T_w2 、流体１、２の熱伝達率をそれぞれh₁ 、h₂ 、円管の熱伝導率をλ 、隔板の厚さをδ 、伝熱面積をA とすれば次の関係式を得る。

\[Q=h_1 \cdot \bigl( T_{f1} - T_{w1} \bigr) \cdot \pi \cdot d_1 \cdot l \hspace{1.3em} (2.7) 　　\]

\[Q=\dfrac{2 \cdot \pi \cdot \lambda \cdot \bigl( T_{w1} - T_{w2} \bigr) }{\ln \dfrac{d_2}{d_1}} \cdot l \hspace{2em} (2.8) \]

\[Q=h_2 \cdot \bigl( T_{w2} - T_{f2} \bigr) \cdot \pi \cdot d_1 \cdot l \hspace{1.5em} (2.9) 　　\]

上式より、T_w1 、T_w2 を消去し整理すると次式を得る。

\[Q=K' \cdot \pi \cdot \bigl( T_{f1} - T_{f2} \bigr) \cdot l \tag{2.10} \]

ここに

\[K'=\dfrac{1}{\dfrac{1}{h_{1} \cdot d_1}+\dfrac{1}{2 \cdot \lambda} \cdot \ln \dfrac{d_2}{d_1} +\dfrac{1}{h_{2} \cdot d_2}} \tag{2.11} \]

K'は線熱通過率と呼ばれ単位が W/mK と熱通過率とは異なる。円管の外表面積Ao を基準にして熱通過率を用いて書き改めると次式となる。

\[Q=K \cdot \bigl( T_{f1} - T_{f2} \bigr) \cdot Ao \tag{2.12} \]

ここに　

\[K=\dfrac{1}{\dfrac{d_2}{h_{1} \cdot d_1}+\dfrac{d_2}{2 \cdot \lambda} \cdot \ln \dfrac{d_2}{d_1} +\dfrac{1}{h_{2}}} \tag{2.13} \]

 

フィンを有する場合の熱通過

　熱交換の効率向上のためにフィンが設けられることが多い。特に、熱伝達率が大きく異なる流体間の熱交換では熱伝達率の小さいほうにフィンを設け、それぞれの熱抵抗を近づける設計がなされる。図 2.3 のように、厚さd の隔板に高さH 、厚さb の平板フィンが設けられている場合の熱通過を考える。

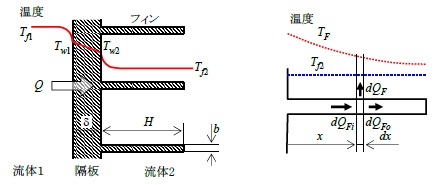
図 2.3 フィンを有する平板の熱通過

流体１側の伝熱面積をA₁ 、流体２側の伝熱面積をA₂ とし伝熱面積A₂ を隔壁に沿った伝熱面積A_wとフィンの伝熱面積A_Fに分けて熱移動量を求めるとそれぞれ次式で表される。

\[Q=h_1 \cdot \bigl( T_{f1} - T_{w1} \bigr) \cdot A_1 \tag{2.14} 　　\]

\[Q=\dfrac{\lambda}{\delta} \cdot \bigl( T_{w1} - T_{w2} \bigr) \cdot A_1 \tag{2.15} \]

\[Q=h_2 \cdot \bigl( T_{w2} - T_{f2} \bigr) \cdot A_w + h_2 \cdot \eta \cdot \bigl( T_{w2} - T_{f2} \bigr) \cdot A_F \tag{2.16} \]

ここに、η はフィン効率で、フィンによる実際の交換熱量とフィン表面温度をフィン根元温度T_w2 とした場合の交換熱量の比で定義される。

上式より、T_w1 、T_w2 を消去し流体２側の伝熱面積をA₂ を基準に整理すると次式を得る。

\[Q=K \cdot \bigl( T_{f1} - T_{f2} \bigr) \cdot A_2 \tag{2.17} \]

ここに

　\[K=\dfrac{1}{\dfrac{A_2}{h_{1} \cdot A_1}+\dfrac{\delta \cdot A_2}{\lambda \cdot A_1}+\dfrac{A_2}{h_{2} \cdot \bigl( A_w + \eta \cdot A_F \bigr)}} \tag{2.18} \]

　

フィン効率を求めるために、フィンからの伝熱を考える。いま、根元からx の距離にある微小長さdxでの熱の釣り合いは、フィンから入ってくる熱量dQ_Fi 、フィンをから出ていく熱量dQ_Fo 、流体２に伝わる熱量dQ_F とすると次式で表される。

\[dQ_F = dQ_{Fi} -dQ_{Fo} \tag{2.19} \]

一般に、フィンの厚さb は高さH に比べて十分小さいく、フィン内の厚さ方向の温度分布は無視できる。したがってフィン温度T_F はx のみの関数となり、フィンの幅を単位長さに取るとフィンの断面積はb となり、上式は次式のように書き換えられる。

\[ dQ_{F} = -\lambda \cdot b \cdot \frac{dT_F}{dx}-\biggl[- \lambda \cdot b \cdot \frac{d}{dx} \biggl( T_F +\frac{dT_F}{dx} dx \biggr) \biggr] =\lambda \cdot b \cdot \frac{d^2 T_F }{dx^2}dx \tag{2.20} \]

一方、dQ_F は流体２との熱交換量から次式で表される。

\[dQ_F = h_2 \cdot \bigl( T_F-T_{f2} \bigr) \cdot 2 \cdot dx \tag{2.21} \]

したがって、次式のフィン温度に対する２階線形微分方程式を得る。

\[ \frac{d^2 T_F}{dx^2} = m^2 \cdot \bigl( T_F-T_{f2} \bigr) \tag{2.22} \]

ここに　\(m^2=2 \cdot h_2 / \bigl( \lambda \cdot b \bigr) \)

この微分方程式の解は積分定数をC₁、C₂ として次式で表される。

\[ T_F-T_{f2}=C_1 \cdot e^{mx} +C_2 \cdot e^{-mx} \tag{2.23} \]

境界条件はフィンの根元および先端を考える。

\[ \bigl( T_F \bigr) _{x=0}=T_{w2} \tag{2.24} \]

\[\bigl( Q_{F} \bigr) _{x=H}=- \lambda \cdot \biggl( \frac{dT_F}{dx} \biggr) \cdot b =h_2 \cdot b \cdot \bigl( T_F -T_{f2} \bigr) \tag{2.25} \]

境界条件より、積分定数をC₁、C₂は次式となる。

\[ C_1=\bigl( T_{w2} -T_{f2} \bigr) \cdot \frac{ \bigl( 1- \frac{h_2}{m \cdot \lambda} \bigr) \cdot e^{-mH } }{e^{mH} + e^{-mH} + \frac{h_2}{m \cdot \lambda} \cdot \bigl( e^{mH} - e^{-mH} \bigr)} \tag{2.26} \]

\[ C_2=\bigl( T_{w2} -T_{f2} \bigr) \cdot \frac{ \bigl( 1+ \frac{h_2}{m \cdot \lambda} \bigr) \cdot e^{mH } }{e^{mH} + e^{-mH} + \frac{h_2}{m \cdot \lambda} \cdot \bigl( e^{mH} - e^{-mH} \bigr)} \tag{2.27} \]

したがって、フィン温度は双曲線関数を用いて整理すると次式を得る。

\[ T_F=T_{f2}+ \bigl( T_{w2}-T_{f2} \bigr) \cdot \frac{\cosh{ \big[ m \cdot \bigl( x-H \bigr) \big] } + \frac{h_2}{m \cdot \lambda } \cdot \sinh{ \big[ m \cdot \bigl( x-H \bigr) \big] } }{\cosh{ \big( m \cdot H \bigr) } + \frac{h_2}{m \cdot \lambda } \cdot \sinh{ \big( m \cdot H \big) }} \tag{2.28} \]

フィンと流体２の交換熱量は、フィン根元の温度勾配より次式で求められる。

\begin{align*} Q_F & =- \lambda \cdot b \cdot \bigg( \frac{dT_F}{dx} \bigg)_{x=0} \notag \\ & =\lambda \cdot b \cdot m \cdot \bigl( T_{w2} - T_{f2} \bigr) \cdot \frac{\sinh{\bigl(m \cdot H \bigr) } + \frac{h_2}{m \cdot \lambda } \cdot \cosh{ \bigl( m \cdot H \bigr) }} {\cosh{\bigl(m \cdot H \bigr) } + \frac{h_2}{m \cdot \lambda } \cdot \sinh{ \bigl( m \cdot H \bigr) } } \tag{2.29} \end{align*}

一方、フィンの温度が根元温度と等しいとした場合の交換熱量Q_F0 は次式で表される。

\[ Q_{F0}=h_2 \cdot \bigl( 2 \cdot H + b \bigr) \cdot \bigl( T_{w2}-T_{f2} \bigr) \tag{2.30} \]

したがって、フィン効率は次式で表される。

\[ \eta=\frac{Q_F}{Q{F0}}=\frac{\lambda \cdot b \cdot m}{h_2 \cdot \bigl( 2 \cdot H + b \bigr) } \cdot \frac{\sinh{\bigl(m \cdot H \bigr) } + \frac{h_2}{m \cdot \lambda } \cdot \cosh{ \bigl( m \cdot H \bigr) }} {\cosh{\bigl(m \cdot H \bigr) } + \frac{h_2}{m \cdot \lambda } \cdot \sinh{ \bigl( m \cdot H \bigr) } } \tag{2.31} \]

一般的な、平板フィンではフィン高さH はフィン厚さb に対し十分高く、フィン素材も銅、アルミニウムのような熱伝導率の高いものが使用される。この場合、フィン先端からの放熱量は無視でき、フィン効率は近似的に次式で求められる。

\[ \eta=\frac{\lambda \cdot b \cdot m}{h_2 \cdot 2 \cdot H } \cdot \frac{\sinh{\bigl(m \cdot H \bigr) } } {\cosh{\bigl(m \cdot H \bigr) } } =\frac{\tanh{\bigl( m \cdot H \bigr)}}{m \cdot H } \tag{2.32} \]