熱伝導率

2025年6月26日更新

熱伝導率

熱伝導率は、熱移動に関連する物理量で、熱交換器の設計には不可欠なものである。粘度と同様に冷凍サイクルあるいはランキンサイクルのように動作温度範囲が広く、相変化を伴うような場合、気液で利用できる相関式が便利である。近年、広範囲に適用できる状態式が規格化されたことにより、熱伝導率の新しい相関式も多く提案されている。代表的なものとして希薄気体の熱伝導率と余剰の熱伝導率を組み合わせた手法と測定データからパラメータの最適手法を用いて直接相関式を求める手法が知られている。R744を例にとると次のような相関式が提案されている。

(1)Huberらの相関式¹⁾

\[ \lambda(\rho,T)= \lambda ^0 (T)+\Delta \lambda(\rho,T) + \Delta \lambda_c (\rho,T) \]

(1.1)

　ここに

\( \lambda^0 \) ：希薄気体の熱伝導率

\( \Delta \lambda \) ：余剰熱伝達率

\( \Delta \lambda_c \) ：臨界点近傍の補正項

\( \rho \) ：密度

\( T \) ：温度

希薄気体の熱伝導率、臨界点近傍の補正項、臨界点近傍の補正項は次式で整理されている。

・希薄気体の熱伝導率

\[ \lambda^0(T)= \frac{{T_r}^{0.5}}{\sum_{k=0}^{2}L_k/{T_r}^k} \]

(1.2)

　ここに

\( T_r \)：対臨界温度 (\( T/T_c \) )

\( L_k \)：係数

・余剰熱伝導率

\[ \Delta \lambda(\rho,T)= \sum_{i=1}^{6} \left( B_{1,i} + B_{2,i} T_r \right) {\rho_r}^i \]

(1.3)

　ここに

\( \rho_r \)：対臨界密度 (\( \rho/\rho_c \) )

\( B_{1,i},B_{2,i} \)：係数

・臨界点近傍の補正項

\[ \Delta \lambda_c(\rho,T)= \frac{\rho C_p R_D k_B T}{6 \pi \eta \xi} \left( \bar{\Omega}-\bar{\Omega}_0 \right) \]

(1.4)

　ここに

(1.5)

\( \bar{\Omega}=\displaystyle \frac{2}{\pi} \left[ \left( \frac{C_p -C_v}{C_p} \right) \arctan(\bar{q}_D \xi ) + \frac{C_v}{C_p} \bar{q}_D \xi \right] \)

(1.6)

\( \bar{\Omega}_0=\displaystyle \frac{2}{\pi} \left[ 1- \exp \left( - \frac{1}{(\bar{q}_D \xi) ^ {-1} + ( \bar{q}_D \xi \rho_c / \rho )^2 /3} \right) \right] \)

(1.7)

\( \xi=\displaystyle \xi_0 \left(\frac{P_c \rho}{\Gamma {\rho_c}^2} \right) ^{\nu /\gamma} \left[ \left( \frac{\partial \rho (T,\rho)}{\partial P} \right) _T - \left( \frac{T_{ref}}{T} \right) \left(\frac {\partial \rho (T_{ref},\rho)}{\partial P} \right)_T \right] ^{\nu/\gamma} \)

\( C_p \)：定圧比熱

\( C_v\)：定容比熱

\( k_B \)：ボルツマン定数

\( T_{ref} \)：参照温度 ( \( 1.5T_{c} \) )

\( \eta \)：粘性率

\( R_D,\nu,\gamma \)：定数

\( \Gamma,\xi _0,\bar{q}_D \)：係数

(2)Scalabrinらの相関式²⁾

\[ \lambda_r= \sum_{i=1}^{3} n_i {T_r}^{g_i} {\rho_r}^{h_i} +\exp(-5 {\rho_r}^2)\sum_{i=4}^{10} n_i {T_r}^{g_i} {\rho_r}^{h_i} + n_c \Delta \lambda_{c} \]

(1.8)

　ここに

(1.9)

\( \lambda_r= \lambda/\Lambda_c \)

(1.10)

\( \Lambda_c=\displaystyle \frac{R^{5/6} {P_c}^{2/3}}{{T_c}^{1/6} M^{1/2}{N_A}^{1/3}} =4.81384 \)

\( \Delta\lambda_c \) ：臨界点近傍の補正項

\( M \) ：分子量

\( N_A \) ：アボガドロ定数

\( P_c \) ：臨界圧力

\( R \) ：ガス定数

\( n_i,g_i,h_i \) ：係数

　臨界点近傍の補正項は次式で整理されている。

\[ \Delta\lambda_c= \frac{\rho _r \exp\{-{\rho}^{a_1} / a_1 - [a_2 (T_r -1 )]^2- [a_3 (\rho_r -1 )]^2 \} } {\left( \left[\{(1-1/T_r) + a_4 [(\rho _r -1) ^2]^{1/2a_5} \}^2 \right]^{a_6} + \left\{ \left[ a_7(\rho_r -\alpha) \right]^2 \right\}^{a_8} \right)^{a_9}} \]

(1.11)

　ここに

(1.12)

\( \alpha = 1- a_{10}\ \text{arccosh} \left\{ 1+ a_{11} [(1-T_r)^2]^{a_{12}} \right\} \)

\( a_i \) ：係数

　Huberらの相関式およびScalabrinらの相関式から算出したR744の飽和液、飽和ガスの熱伝導率を図1.1、臨界温度近傍の熱伝導率を図1.2に示す。

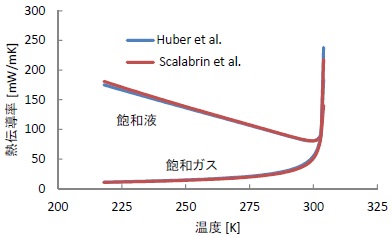
図1.1　R744の飽和液、ガスの熱伝導率

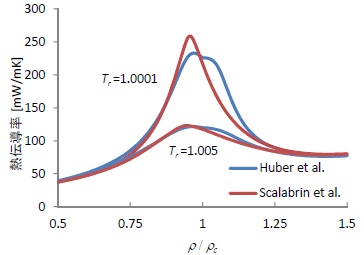
図1.2　臨界温度近傍の熱伝導率

　両者の相関式の偏差は飽和液で最大3%、飽和ガスで最大7%である。熱伝導率の測定値は粘性率よりさらにばらつきが大きく、相関に用いた主データの違いと推定されるが、測定データのばらつき範囲にある。両者の特徴は臨界点近傍の補正項にあり、Huberらは半理論式、Scalabrinらは測定値の相関で作成している。半理論式は少ないデータから相関式を作ることができ多くの物質で使用されるようになった。しかし、図1.2から分かるようにHuberらの相関式から算出した臨界点直近の熱伝導率は異常な挙動を示している。算出に用いた状態式³⁾の臨界点近傍の挙動、特に比熱が正しくあらわされていないために生じる現象である。また、粘性率も関数に含まれるために、精度の高い状態式に加え粘性率も必要になる。

　熱伝導率の相関式も、状態式あるいは粘度の相関式と同様に、三重点から超臨界までの幅広い温度、密度に適用できる相関式が提供されるようになってきている。しかし、混合物も含めまだまだ不足しており、推算に頼る以外にない。熱伝導率の推算のために、多くの手法が提案されているが、測定値がある場合、対応状態原理と組み合わせて使用するのが比較的信頼性が高いと考えられる。

ページトップ