2025年6月26日更新

  希薄気体の熱伝導率\( \lambda^0 \) は、多原子分子では分子の並進運動の項と内部エネルギの項に分けた次式で表される。

　ここに

\( {C_p}^0 \) ：希薄気体の比熱

\( f_{int} \) ：内部エネルギに関する因子

\( M \) ：分子量

\( R \) ：ガス定数

η⁰：希薄気体の粘度

\( f_{int} \) を0.001とおいた場合をオイケン相関式、0.00132とおいた場合を修正オイケン式と呼ばれる。実際の物質では温度の関数となる。主な冷媒の\( f_{int} \) を以下に示す⁴⁾⁵⁾⁶⁾。

　　R32 : 8.1980×10^-4 + 2.2352×10^-7T

　　R125 : 1.2565×10^-3 + 2.22296×10^-6T

　　R134a : 1.32×10^-3

　　R143a : 1.0066×10^-3 + 1.3729×10^-6T

　　R290 : 1.0398×10^-3 + 5.4024×10^-7T

　　R744 : 7.0793×10^-4 + 1.3194×10^-6T

上記\( f_{int} \) を用いて算出した希薄気体の熱伝導率を図2.1に示す。

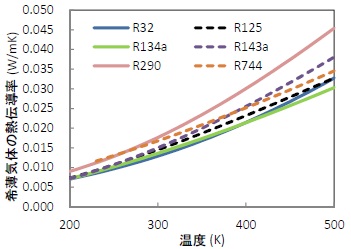
図2.1　希薄気体の熱伝導率

　混合気体の熱伝導率についは、McLindenら⁴⁾は次式を用いて算出している。

\( {\lambda^0}_m \) ：混合物の希薄気体の熱伝導率

\( y_i \) ：組成iのモル分率

\( {\lambda^0}_i \) ：組成iの希薄気体の熱伝導率

\( \phi_{ij} \) ：相互作用パラメータ

相互作用パラメータは次式で表される。

　ここに

\( {\lambda^0}_i \) ：組成iの希薄気体の粘度

\( M_i \) ：組成iの分子量

　式(2-3)は粘度の相互作用パラメータと同一であるが、単原子分子の熱伝導率と粘度の関係から導きだされたもので、あくまで近似式である。

上記、混合則を用いて算出した混合冷媒の希薄気体の熱伝導率を図2.2に示す。

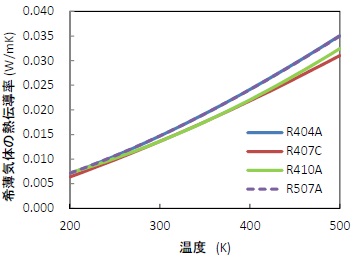
図2.2　混合冷媒の希薄気体の熱伝導率

ページトップ