2025年6月26日更新
対応状態原理による余剰熱伝導率の推算
対応状態原理による余剰熱伝導率の推算方法としては、粘性率と同様にHelmholtzエネルギと関連させた拡張対応状態原理が提案されている4)5)6)。拡張対応状態原理による余剰熱伝導率Δλは、参照物質を下付き添え字0で表すと次式で算出される。
ここに
\( T_0 = T /f \)
\( \rho_0 = \rho h \)
\( F_{\lambda} = f^{1/2} h^{-2/3} \left( M_0 /M \right) ^{1/2} \)
\( f \) :温度換算係数
\( h \) :密度換算係数
\( T_0 , \rho_0 \) は対象物質の偏倚Helmholtzエネルギ\( \phi ^r \)および圧縮係数\( Z \)から次式が満足するように算出する。
対象物質の実測値がある場合には、式(3.1)の\( \rho_0 \) の代わりに次式の\( \rho_{0,v} \) を用いることで熱伝導率推算の精度向上を図る。
ここに
\( \chi \):形状係数
拡張対応原理での推算の精度を熱物性ハンドブック7)に記載されているR125の希薄気体と飽和液の熱伝導率を用いて算出した形状係数とHuberらのR125の相関式8)を用いて算出した熱伝導率を比較する。参照物質としてR134aとR290を用いて算出した形状係数を図3.1、Huberらの相関式および形状係数から算出した飽和液の熱伝導率を図3.2に示す。また、飽和液と温度500Kでの熱伝導率のHuberらの相関式との偏差を図3.3、3.4に示す。
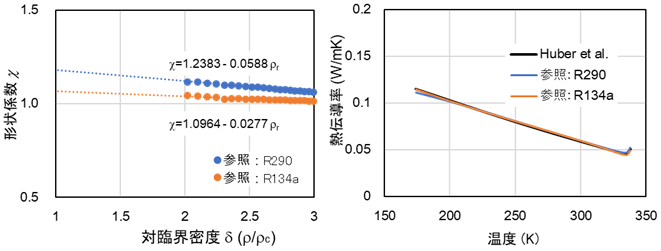
図3.1 R125の形状係数図3.2 飽和液の熱伝導率
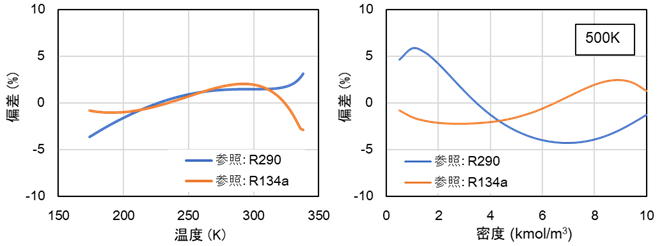
図3.3 飽和液の偏差図3.4 500Kでの偏差
形状係数から算出した熱伝導率とHuberらの相関式を比較すると参照物質 R290及びR134aとも偏差は小さく、実用的には十分な精度と考えられる。特にR134aは飽和液、500Kともに3%以下の偏差となっている。熱伝導率の誤差の大きな要因の臨界点近傍の増加を同一の式を用いたことと余剰熱伝導率が温度の影響が少ないことが考えられる。
混合物質についても、純物質から拡張対応原理を用いて推算手法が報告されているが、混合冷媒は組成が固定されているために、純物質と同様の手法が取れると考えられる。主に使用されている混合冷媒の形状係数を図3.5に示す。算出に使用したデータは冷凍空調便覧(第6版)、Leeら及び高仙峰の飽和液の熱伝導率9)10)11)である。
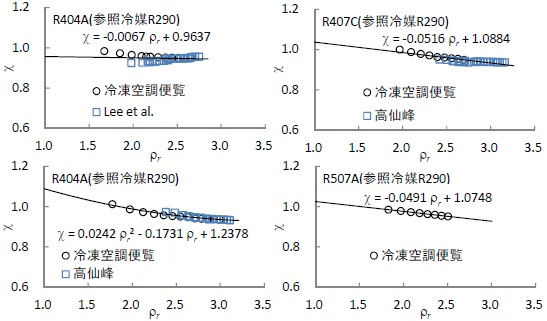
図3.5 混合冷媒の形状係数
冷 凍
冷 媒
湿り空気
伝 熱
地球環境
データ集
