地球温暖化

更新日:2023年12月31日更新

地球の温度

地表の気温変化

近年の世界および日本の年平均気温の推移を図1-1、日本近郊の二酸化炭素濃度の推移を図1-2に示す。平均気温の推移は1991～2020年の平均値からの偏差を用いている。

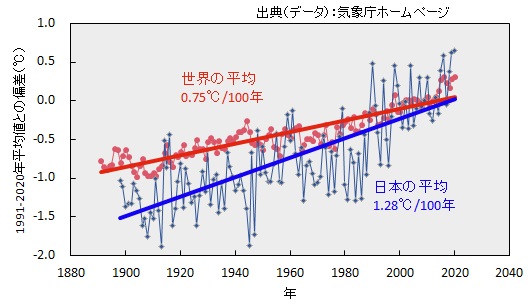
図1-1 年平均気温の推移

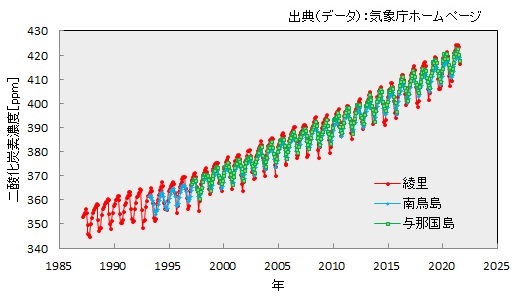
図1-2 大気中の二酸化炭素濃度の推移

平均気温の変化は単調ではないが130年を通してみれば右上がりの傾向になっている。これらのデータを単純に一次式で回帰すると、世界平均では0.75℃/100年、日本平均(15都市)では1.28℃/100年の勾配になる。したがって、2020年では世界平均で1℃、日本平均で1.7℃の温暖化になっている。日本平均の勾配が高いのは緯度が高く、エネルギの大量消費によるヒートアイランド化の影響と考えられる。温暖化によって、極地の氷河の氷解、異常気象等が多くなっている。国内においても、大雨に関する特別警報が運用が開始された2013年以来毎年発令されている。特別警報は本来数十年に一度の災害とされるものであり異常気性が恒常的になっている。日本の平均気温は、世界のそれと比べて毎年のばらつきが大きく1℃以上の変化もある。温暖化傾向にあるものの寒冷化のリスクも消えていない。1993年には平成の米騒動と言われる冷夏による米不足が発生している。1933、1934年の東北凶作のような悲惨な結果にはならなかったが国際的な米市場を混乱させた。
温暖化の原因として指摘されているのが、人為的に排出される二酸化炭素をはじめとする温室効果ガスである。二酸化炭素の濃度は図1-2に示すように季節要因を除けば単調増加であり、産業革命前の280ppmに対し、既に約1.5倍の濃度になっている。このままいけば、2050年までに1.5℃を超えてしまう。パリ協定の追及目標である御度上昇を1.5℃以下にするためには、世界全体の人為的な二酸化炭素の正味排出量を、2030年までに2010年水準から45%削減、2050年に正味ゼロにする必要がある。2021年以降のパリ協定に基づいた先進国の削減計画では、1.5℃に抑える排出量に沿っている。

近年の温度上昇を象徴するものとして「ホッケースティック曲線」がIPCCの第3次報告書で用いられた。過去1000年の気温が緩やかに下がり、20世紀になり突然上昇する形がホッケーのステックを横に置いた形に似ていることから呼ばれたものであるが、懐疑論も多く第4次報告書以降は類似の別の図に差し替えられた。しかし、平均気温の大きな変化は無かったとされる1000年でも、冷夏、旱魃、長雨等の異常気象による飢饉は頻繁にあった。また、地球の尺度で気温を見ると常に変化している。図1-3に南極の氷床から推測された過去80万年の気温を示す。およそ10万年周期で氷河期と間氷河期を繰り返し、温度変化は10℃以上に達している。先の氷河期が終了後の温度上昇は6000年前まで続き、日本では縄文海進と呼ばれるれ、海岸線が内陸県の埼玉県に達していた。温室効果ガスによる人為的な温暖化は新たな課題であるが、自然的なものも含め社会全体のリスクをいかに少なくするかが課題である。

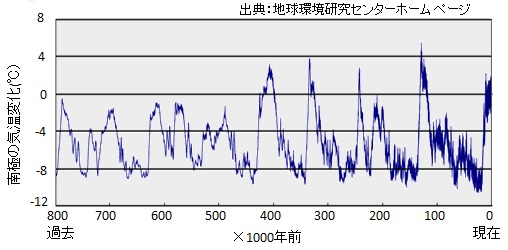
図1-3 南極の温度変化

温室効果ガスの影響

地球の熱収支

太陽から地球が受ける輻射エネルギを100とした熱収支を図1-4に示す。

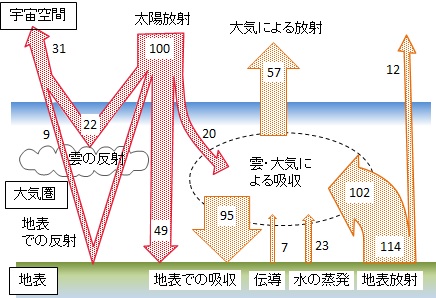
図1-4 地球の熱収支

地球の反射率（アルベド）は常に変化するが、雲が50%、地表面のうち雪原が80%、地面が7〜20%、海面は10%以下で地球全体としては30%程度である。一方、太陽からの放射エネルギのうち約20%が大気、雲に吸収されるのに対し。地表からの放射エネルギは90%近くが大気、雲に吸収される。両者の違いは輻射源の温度による放射されるエネルギの波長の違いによる。ウィーンの変位則から太陽放射のピーク波長は500nmに対し、地球放射のピーク波長は10000nmとなり、水蒸気、二酸化炭素に吸収されやすい。

温室効果ガスがない場合

大気がない場合、あるいは1原子分子あるいは等核二子分子のように熱的に透明である場合、地表の温度は太陽から地球に入るエネルギと地球から放射されるエネルギから容易に算出される。

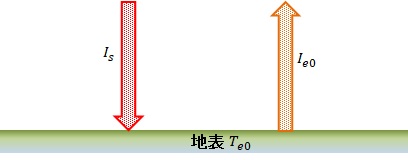
図1-5 大気がない場合の熱収支

地表を基準とした単位面積当たりの太陽から地球に入るエネルギI_sは、太陽定数をS、地球の反射率をρとすると次式で算出できる。

\[ I_s= \bigl( 1 - \rho \bigr) \cdot S / 4 \tag{1.1} \]

一方、地表からの単位面積当たりの放出エネルギ流束I_e₀は、温度をT_e₀、ステファン・ボルツマン定数をσとすると次式で算出できる。

\[ I_{e0}= \sigma \cdot {T_{e0}} ^ 4 \tag{1.2} \]

したがって、\(I_s=I_{e0} \) とすると地表温度は次式で算出できる。

\[ T_{e0}= \bigl[ \bigl( 1 - \rho \bigr) \cdot S / \big(4 \sigma \big) \bigr ] ^ {0.25} \tag{1.3} \]

太陽定数は周期的に変動するが変動幅は少なく、大気がない場合の地表の温度は反射率で決まる。太陽定数を1366kW/m²、ステファン・ボルツマン定数 = 5.67E-8 W/m²K、反射率を現状の0.3とすると地表の温度は255K(-18℃)となる。温室効果ガスがない場合の地球の平均気温は255Kであるとの記載をよく見かけるが、あくまでも反射率が0.3のときであり、平均気温が255Kになれば、極地から海水は凍り、地表は氷で覆われ反射率がさらに大きくなり、平均温度がさらに低下する。地球全体が氷原とすると反射率は約0.8であり平均温度は183K (-90℃)程度になる。現在有力視されている地球全体が凍結したスノーボールアース仮説は、温室効果ガスが極めて少なくなれば実現することが容易に推測できる。現在、二酸化炭素の吸収量と排出量が平衡するカーボンニュートラルの意味で脱炭素という言葉が使われているが、大気中の二酸化炭素がなくなれば、地表は極低温になるばかりでなく、光合成も不可になり生物が生存できなくなる。適量の二酸化炭素を含めた温室効果ガスはすべての生物に必要不可欠なものであり、脱炭素のような誤解を招く言葉を使うのはいかがなものか。漢字的な表現を使うなら衡炭素あたりが妥当と考える。

温室効果ガスが一層の場合

実際の温室効果ガスは大気中に分布し相互にエネルギ授受があるが、計算が容易になるように、太陽光の吸収率をα、地表からの放射エネルギの吸収率をβ の薄い一層の温室効果ガスを考える。

図1-6 温室効果ガスが一層の熱収支

地表および温室効果ガス層での熱収支は次式となる。

\[ \bigl( 1 - \alpha \bigr) \cdot I_s +I_{g} = I_{e1} \tag{1.4} \]

\[ \alpha \cdot I_s + \beta \cdot I_{e1}= 2 I_{g} \tag{1.5} \]

ここで、大気がないときの地表温度を用いれば\( I_s=\sigma \cdot {T_{e0}}^4 \)となり、式(1.4)(1.5)を各温度を用いて整理すると次式を得る。

\[ T_{e1} =\left( \frac{2-\alpha}{2-\beta} \right) ^{0.25} \cdot T_{e0} =\left[ \frac{2-\alpha}{2-\beta} \cdot \frac{\left( 1 - \rho \right) \cdot S}{4 \sigma} \right] ^{0.25} \tag{1.6} \]

\[ T_{g}=\left( \frac{\alpha+\beta-\alpha\beta}{2-\beta} \right) ^{0.25} \cdot T_{e0} =\left[ \frac{\alpha+\beta-\alpha\beta}{2-\beta} \cdot \frac{\left( 1 - \rho \right) \cdot S}{4 \sigma} \right] ^{0.25} \tag{1.7} \]

上式に現状値の\( \alpha =0.29 \) 、\( \beta =0.89 \) 、\( \rho =0.3 \) を入れて計算すれば地表温度284K（11℃）、大気温度243K(-30℃）となり、現在の地表の平均温度287K(14℃)からみれば一層モデルでは温室効果を過少に評価することになるが、手計算でもできる簡単なモデルで温室効果ガスの影響を表すことができる。温室効果が最大になるのは太陽光の吸収率がゼロ、地表からの放射エネルギの吸収率が100%の時で、この時の地表の受ける輻射エネルギは2倍になる。ちなみに、温室効果ガスがN層のモデルでは（N+1)倍になる。一方、太陽光の吸収率と地表からの放射エネルギの吸収率が同じであれば、温室効果は生じない。

温室効果ガスが二層の場合

温室効果ガスが薄い二層になっている時を考える。太陽光の吸収率および地表からの放射エネルギの吸収率は各層で同一でそれぞれα、βとする。

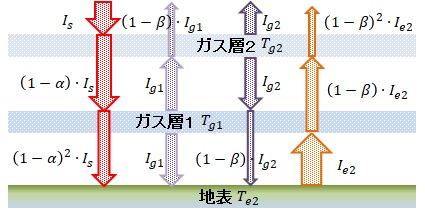
図1-7 温室効果ガスが二層の熱収支

地表、温室効果ガスの第１層、第２層の熱収支から次式を得る。

\[ \left( 1-\alpha \right)\cdot I_s + I_{g1} + \left( 1-\beta \right)\cdot I_{g2} = I_{e2} \tag{1.8} \]

\[ \alpha \cdot \left( 1-\alpha \right) \cdot I_s + \beta \cdot I_{g2} + \beta \cdot I_{g2} = 2 \cdot I_{g1} \tag{1.9} \]

\[ \alpha \cdot I_s + \beta \cdot I_{g1} + \beta \cdot \left( 1- \beta \right) \cdot I_{g2} =2 \cdot I_{g2} \tag{1.10} \]

(1.8)～(1.9)式を温室効果ガスが一層の場合と同様にして解と各温度は次式となる。

\[ \begin{align} T_{e2} &=\left( \frac{\alpha ^2 - \alpha \cdot \beta - 2\cdot \alpha + \beta +2}{2-\beta} \right) ^{0.25} \cdot T_{e0} \\ &=\left[ \frac{\alpha ^2 - \alpha \cdot \beta - 2\cdot \alpha + \beta +2}{2-\beta} \cdot \frac{\left( 1 - \rho \right) \cdot S}{4 \sigma} \right] ^{0.25} \tag{1.11} \end{align} \]

\[ \begin{align} T_{g1} &=\left( \frac{\alpha ^2 \cdot \beta - \alpha ^2 - \alpha \cdot \beta ^ 2 -\alpha \cdot \beta + \alpha + \beta ^2 + \beta }{2-\beta} \right) ^{0.25} \cdot T_{e0} \\&=\left[ \frac{\alpha ^2 \cdot \beta - \alpha ^2 - \alpha \cdot \beta ^ 2 -\alpha \cdot \beta + \alpha + \beta ^2 + \beta }{2-\beta} \cdot \frac{\left( 1 - \rho \right) \cdot S}{4 \sigma} \right] ^{0.25} \tag{1.12} \end{align} \]

\[ \begin{align} T_{g2} &=\left( \frac{\alpha + \beta -\alpha \cdot \beta}{2-\beta} \right) ^{0.25} \cdot T_{e0} =\left[ \frac{\alpha + \beta -\alpha \cdot \beta}{2-\beta} \cdot \frac{\left( 1 - \rho \right) \cdot S}{4 \sigma} \right] ^{0.25} \tag{1.13} \end{align} \]

上式に現状値の\( \alpha =0.29 \) 、\( \beta =0.89 \) 、\( \rho =0.3 \) を入れて計算すれば地表温度300K(27℃)、温室効果ガス第一層274K（0℃）、第二層243K（-30℃）となる。現状の地表温度より高くなるが、このモデルでは地表から大気への熱伝導、水の蒸発によるエネルギ移動は考慮されていない。また、吸収率を各層で一定としたが実際には温度、圧力が異なるために吸収率も異なる。正確な温度上昇を計算するためには雲の動きを含めた詳細なモデルの構築と膨大な計算を行う必要がある。

ページトップ

二