2025年6月26日更新
気液平衡計算
気液平衡条件
圧力\( P \) 、温度\( T \) で相平衡時には、Gibbsエネルギ\( G \) が最小になる。全モル数を\( n \) 、1mol当たりの自由エネルギを\( g \) とすると気液平衡の条件は次式で表される。
多成分系の自由エネルギの変化を全微分で表示すると次式となる。
気液平衡時には温度、圧力が一定であるために、液相を「’」、気相を「’’」で表すと次式を得る。
ここで、気相のモル数の増加は液相のモル数の減少に等しいために式(3.3)は次式に書き改められる。
式(3.4)が常に成立するためには各成分iで次式が成立しなければならない。
式(3.5)の左辺、右辺の物理量は化学ポテンシャル\( \mu \) とも呼ばれ、気液平衡時は、圧力、温度が一定で、各成分の化学ポテンシャルが気液で等しくなる。
気液平衡計算では、化学ポテンシャルの代わりに次式で定義されるフガシティ\( f_i \) とフガシティ係数\( \varphi_i \)を用いる。
また、混合物中の成分\( i \) のフガシティ係数\( \hat{\varphi}_i \) は次式で定義される。
ここに
\( \hat{f}_i \) :混合物中の成分\( i \) のフガシティ
気液平衡計算
気液計算には、露点、沸点の計算と二相内の特定点の二種類がある。これらの計算は蒸 留等で広く利用されており、特に三次元状態式を用いた計算手法は多くの文献が出されて いる。ここでは、一つの例として、系の組成と温度から沸点圧力の計算手法と系の組成と 温度、圧力から気液の組成の計算手法について記載する。これらの計算手法はHelmholtz 型状態 式にも適用できる。ただし、収束は遅い。
◆沸点圧力の計算
(1) 沸点温度\( T \) 、系の組成 \( z_i \) を与える。
(2) 沸点圧力\( P_b \) 、気相のフガシティ係数\( \hat{\varphi}_{Vi} \)を仮定。
気相のフガシティ係数\( \hat{\varphi}_{Vi} \)はすべての組成で 1 あるいは 0.8 とおく。
(3) 液相組成 \( x_i \)(=系の組成 \( z_i \) )、温度 \( T \)、圧力 \( P_b \)から液相のフガシティ \( \hat{f}_{Li} \) を算出。
(4)液相のフガシティ\( \hat{f}_{Li} \) 、気相のフガシティ係数\( \hat{\varphi}_{Vi} \) 、圧力 \( P_b \)から気相組成\( y_i \)を算出。
(5) 気相組成 \( y_i \)、温度\( T \)、圧力\( P_b \) から気相のフガシティ\( \hat{\varphi}_{Vi} \) を算出。
(6) \( P_{b \ new}=P_b + \Delta P \)
とし、各組成のフガシティが気液で等しくなるまで(3)~(6) を繰り返す。
指数\( pn \) は1とし、収束しない場合は小さくする。臨界点近傍を除き 0.5 ではほとんどの系で収束する。
◆気液組成の計算
(1) 温度\( T \)、圧力\( P \)、系の組成 \( z_i \)を与える。
(2) 気液平衡比\( K_i \)の仮定。
気液平衡比\( K_i \) の初期値は次式を用いる。
(3) 系の組成 \( z_i \) 、気液平衡比 \( K_i \)から気相の割合 \( Q_V \) を算出。
・2成分の系
・3成分以上の系
\( Q_V=0.5 \) を初期値とし、 \( \sum (x_i -y_i)=0 \) まで以下を繰り返す。
(4) 液相組成 \( x_i \) 、気相組成 \( y_i \) の算出。
(5) 液相組成\( x_i \) 、温度\( T \) 、圧力\( P \) から液相のフガシティ\( \hat{f}_{Li} \) を算出。
(6) 気相組成 \( y_i \) 、温度\( T \) 、圧力\( P \) から気相のフガシティ\( \hat{f}_{Vi} \) を算出。
(7) \( K_{i \ new}=K_i (\hat{f}_{Li} / \hat{f}_{{Vi}}) \) とし、各組成のフガシティが気液で等しくなるまで(3)~(7)を繰り返す。
気液平衡物性の近似式
気液平衡条件から物性を求める場合、繰り返し計算が多くなる。これを避けるために、開発ツールRCYCLEでは以下の近似式を用いている。 純物質では、気相、液相の物性は一定であるために必要となる気液平衡計算は蒸気圧のみである。蒸気圧の相関式は種々提案されているが、三重点から臨界点まで高精度に相関できる次式で表されるWagner型の飽和蒸気圧力式を用いる。
ここに
\( P_r \) :対臨界圧力
\( T_r \) :対臨界温度
\( \tau \) :換算温度差\( (1-T_r) \)
\( c_{si}, \ t_i \) :係数
ここで、\( \tau と T_r\dot \ln(P_r) \) の関係を示すと図3.1のようになる。図から分かるように、高温あるいは高圧ではほぼ直線になる。したがって、\( n=1,/ t_i \) とし、 偏心係数と組み合わせることにより式3.9を得る。
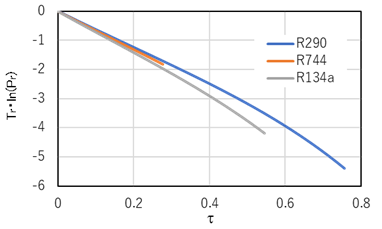
図3.1 \( \tau と T_r\dot \ln(P_r) \) の関係
ただし、混合冷媒の臨界点近傍では直線とはならず、温度勾配の大きいR407Cでは図3.2に示すように独特の軌跡となる。露点、沸点曲線はLemmon らの式と、混合測から計算された沸点、露点から作成した相関式の両者を記載している。臨界点近傍の沸点にわずかな違いがあるが、両者とも温度と圧力の臨界点が異なる。臨界点近傍の物性計算には注意が必要である。
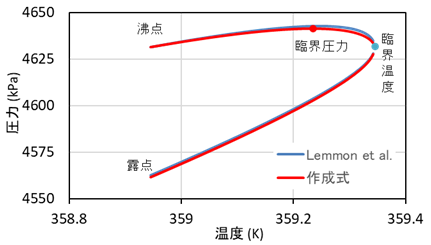
図3.2 R407Cの臨界点近傍の飽和線
混合物質の場合、気相、液相の組成が変化するために、乾き度と物性が直線関係にならない。このために、乾き度および液相、気相の密度、エンタルピ、エントロピを以下の式を用いて算出している。
・乾き度\( x_q \)
ここに
\( x_0 =(T-T^{'})/(T^{'}-T^{''}) \)
\( T^{'} \) :圧力\( P \)での沸点温度
\( T^{''} \) :圧力\( P \)での露点温度
\( c_{xi},\ q_i, \ ,p_i \) :係数
・液相の密度、エンタルピ、エントロピ
ここに
\( X_{sl} \) : 液相の密度、エンタルピ、エントロピ
\( X^{'} \) :圧力\( P \)での沸点の密度、エンタルピ、エントロピ
\( c_{xli},\ q_{xli}, \ ,p_{xli} \) :係数
・気相の密度、エンタルピ、エントロピ
ここに
\( X_{sv} \) : 気相の密度、エンタルピ、エントロピ
\( X^{''} \) :圧力\( P \)での露点の密度、エンタルピ、エントロピ
\( c_{xvi},\ q_{xvi}, \ ,p_{xvi} \) :係数
冷 凍
冷 媒
湿り空気
伝 熱
地球環境
データ集
