流体の流れ方向と熱伝達

流体間の熱伝達は、流体相互間の流れに大きく依存する。基本となる並流、交流、直交流について記載する。

並流

流体Aと流体Bが長さl 、幅b の隔板を介して同一方向に流れている場合の伝熱を考える。流体A、流体Bの質量流量はそれぞれG_A 、G_B 、比熱はc_pA 、c_pB 、入口温度はT_A₁ 、T_B₁ 、出口温度はT_A₂、T_B₂ とする。ここで、比熱c_pA 、c_pB は温度によらず一定とする。

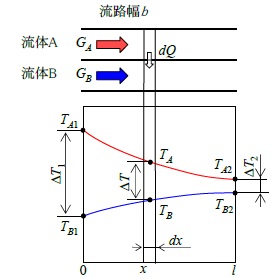
図 3.1　並流の伝熱

入口から\(x \) の位置から微小長さdx での交換熱量は次式で計算できる。

\[dQ=K \cdot \bigl( T_A -T_B \bigr) \cdot dA \tag{3.1} \]

ここに、K は熱通過率、T_A 、T_B は流体A,Bの温度、dA は微小面積( =b･dx ) である。

　一方、dx での伝熱量dQ による流体A、流体B、の温度変化は次式で算出できる。

\[dT_A=- \dfrac{dQ}{G_A \cdot c_{pA}} \tag{3.2} \]

\[dT_B= \dfrac{dQ}{G_B \cdot c_{pB}} \tag{3.3} \]

したがって、dx での温度差の変化は次式となる。

\[dT_A-dT_B = d \bigl( T_A-T_B \bigr)= - \biggl( \dfrac{1}{G_A \cdot c_{pA}} + \dfrac{1}{G_B \cdot c_{pB}} \biggr) \cdot dQ \tag{3.4} \]

ここで \(D=\biggl( \dfrac{1}{G_A \cdot c_{pA}} + \dfrac{1}{G_B \cdot c_{pB}} \biggr) \) とおき、上式に式 (3.1) を代入し整理すると次式が得られる。

\[\frac{d \bigl( T_A-T_B \bigr)}{T_A-T_B}=\frac{d \bigl( \Delta T)}{\Delta T} = - D \cdot K \cdot dA = - D \cdot K \cdot b \cdot dx \tag{3.5} \]

式(3.5)を0～x の範囲で積分する。

\[\int_{\Delta T_1}^{\Delta T} \frac{d \bigl( \Delta T)}{\Delta T} = - D \cdot K \cdot b \cdot \int_{0}^{x} dx \]

\[\ln \frac{ \Delta T}{\Delta T_1} = - D \cdot K \cdot b \cdot x \tag{3.6} \]

したがって

\[\Delta T = \Delta T_1 \cdot \exp{\bigl(- D \cdot K \cdot b \cdot x \bigr) }\tag{3.7} \]

流体A、Bの交換熱量は式(3.1)を0～l まで積分することで求められる。

\[Q= K \cdot b \cdot \Delta T_1 \cdot \int_{0}^{l} \exp{\bigl(- D \cdot K \cdot b \cdot x \bigr)} \cdot dx =\frac{\Delta T_1}{D} \cdot \big[ 1- \exp \bigl(- D \cdot K \cdot b \cdot l \bigr) \big] \tag{3.8} \]

ここで、式(3.6)より　\( \ln ( \Delta T_2 / \Delta T_1) = - D \cdot K \cdot b \cdot l \) 、また、\(A = b \cdot l \) を用いて整理すると次式を得る。

\[Q = K \cdot A \cdot \Delta T_m \tag{3.9} \]

ここに　ΔT_m は対数平均温度と呼ばれ次式で表される。

\[ \Delta T_m = \frac{\Delta T_1 - \Delta T_2}{\ln \bigl( \Delta T_1 \big/ \Delta T_2 \bigr)} \tag{3.10} \]

　流体の流量、出入口温度から伝熱面積を求める場合は上式から容易に算出できるが、流体の流量、入口温度、伝熱面積から出口温度（熱交換量）を求める場合は繰り返し計算が必要となる。このために、出口温度を温度効率から算出する手法が知られている。流体A、Bに対し温度効率ε_A 、ε_B は次式で定義される。

\[\epsilon_A= \biggl| \frac{T_{A1}-T_{A2}}{T_{A1}-T_{B1}} \biggr| \hspace{3em} \epsilon_B= \biggl| \frac{T_{B1}-T_{B2}}{T_{A1}-T_{B1}} \biggr| \hspace{3em} \tag{3.11} \]

熱交換量は流体Aの温度変化から次式で求められる。

\[Q = G_A \cdot c_{pA} \cdot \bigl( T_{A1} - T_{A2} \bigr) =G_A \cdot c_{pA} \cdot \epsilon_A \cdot \bigl( T_{A1} - T_{B1} \bigr) \tag{3.12} \]

上式を式(3.8)に代入し整理すると温度効率<ε_Aは次式で算出できる。

\[\epsilon_A = \frac{T_{A1}-T_{A2}}{T_{A1}-T_{B1}} = \frac{1- \exp \bigl[ -NTU_A \cdot \bigl(1+R \bigr) \bigr]}{1+R} \tag{3.13} \]

ここに

\[NTU_A = \frac{K \cdot A}{G_A \cdot c_{pA}} \tag{3.14} \]

\[R = \frac{G_A \cdot c_{pA}}{G_B \cdot c_{pB}} \tag{3.15} \]

NTU_A は移動単位数と呼ばれる無次元数であり、熱コンダクタンスと熱容量流量（水当量とも呼ばれる）の比である。

流体Bの温度効率ε_Aは次式で算出できる。

\[\epsilon_B = \frac{T_{B2}-T_{B1}}{T_{A1}-T_{B1}} = R \cdot \epsilon _A \tag{3.16} \]

向　流

　並流と同様に、流体Aと流体Bが長さl 、幅b の隔板を介して向流している場合の伝熱を考える。流体A、流体Bの質量流量はそれぞれG_A 、G_B 、比熱はc_pA 、c_pB 、入口温度はT_A₁ 、T_B₁ 、出口温度はT_A₂、T_B₂ とする。

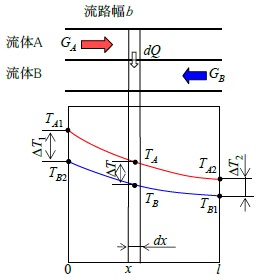
図 3.2　向流の伝熱

入口からx の位置から微小長さdx での交換熱量は次式で計算できる。

\[dQ=K \cdot \bigl( T_A -T_B \bigr) \cdot dA \tag{3.17} \]

　一方、dx での伝熱量dQ による流体A、流体B、の温度変化は次式で算出できる。

\[dT_A=- \dfrac{dQ}{G_A \cdot c_{pA}} \tag{3.18} \]

\[dT_B= -\dfrac{dQ}{G_B \cdot c_{pB}} \tag{3.19} \]

したがって、dx での温度差の変化は次式となる。

\[dT_A-dT_B = d \bigl( T_A-T_B \bigr)= - \biggl( \dfrac{1}{G_A \cdot c_{pA}} - \dfrac{1}{G_B \cdot c_{pB}} \biggr) \cdot dQ \tag{3.20} \]

ここで \(D=\biggl( \dfrac{1}{G_A \cdot c_{pA}} - \dfrac{1}{G_B \cdot c_{pB}} \biggr) \) とおけば並流と同一の式が得られる。したがって、流体A，Bの温度差ΔT は次式となる。

\[\Delta T = \Delta T_1 \cdot \exp{\bigl(- D \cdot K \cdot b \cdot x \bigr) }\tag{3.21} \]

流体A、Bの交換熱量は式(3.1)を0～l まで積分し整理することで、並流と同一の式となる。

\[Q = K \cdot A \cdot \Delta T_m \tag{3.22} \]

ここに　

\[\Delta T_m = \frac{\Delta T_1 - \Delta T_2}{\ln \bigl(\Delta T_1 \big/ \Delta T_2 \bigr)} \tag{3.23} \]

また、向流の場合の温度効率は次式で表される。

\[\epsilon_A = \frac{T_{A1}-T_{A2}}{T_{A1}-T_{B1}} = \frac{1- \exp \bigl[ -NTU_A \cdot \bigl(1- R \bigr) \bigr]}{1 - R \cdot \exp \bigl[ -NTU_A \cdot \bigl(1- R \bigr) \bigr]} \tag{3.24} \]

\[\epsilon_B = \frac{T_{B2}-T_{B1}}{T_{A1}-T_{B1}} = R \cdot \epsilon _A \tag{3.25} \]

直交流

　二つの流体が直交して熱交換する場合、流路の断面で流体が混合するかしないかで大きく伝熱量が異なる。基本的な流れ形式として図 3.3に示す三種類がある。

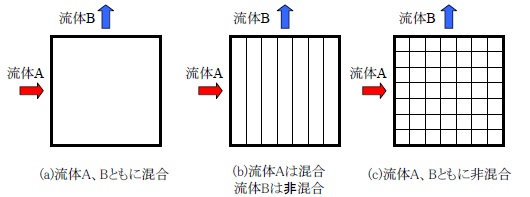
図 3.3 直交流の流れの形式

解析解が得られる流体A、Bともに混合の場合と、一方のみ混合の場合を以下に記載する。

(a)両流体が混合する場合

　流体A、Bが長さX ,高さY の隔板を介して熱移動する場合を考える。流体A、流体Bの質量流量はそれぞれG_A 、G_B 、比熱はc_pA 、c_pB 、流体Aの入口温度をT_A₁ 、出口温度をT_A₂ 流体Bの入口温度をT_B₁ 、出口温度をT_B₂ とする。

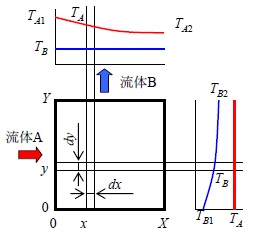
図 3.4　両流体が混合する場合の熱伝達

x 、y の位置から微小面積dx・dy での交換熱量は次式で表される。

\[dQ=K \cdot \bigl( T_A -T_B \bigr) \cdot dx \cdot dy \tag{3.26} \]

流体A,Bともに混合するために、T_A はx のみの関数、T_B はy のみの関数となり、全交換熱量は次式となる。

\[Q=K \cdot X \cdot Y \cdot \bigl( T_{Am} -T_{Bm} \bigr) \tag{3.27} \]

ここに

\[ T_{Am}=\frac{1}{X} \cdot \int_{0}^{X} T_A \cdot dx \tag{3.28} \]

\[ T_{Bm}=\frac{1}{Y} \cdot \int_{0}^{Y} T_B \cdot dy \tag{3.29} \]

微小長さdy についてx = 0 からX まで積分した交換熱量は、流体Bの温度変化となるために以下の式が得られる。

\[K \cdot dy \int_{0}^{X} \bigl( T_A -T_B \bigr) \cdot dx =K \cdot dy \cdot X \cdot \bigl( T_{Am} -T_B \bigr) =G_B \cdot c_{pb} \cdot dT_B \tag{3.30} \]

したがって

\[\frac{dT_B}{dy}=\frac{K \cdot X}{G_B \cdot c_{pB}} \cdot \bigl( T_{Am} - T_B \bigr) \tag{3.31} \]

上式を境界条件 y=0 でT_B=T_B₁ で0からyまで積分すると

\[ T_{Am} -T_B = \bigl(T_{Am} -T_{B1} \bigr) \cdot \exp \biggl[- \biggl( \frac{K \cdot X}{G_B \cdot c_{pB}} \biggr) \cdot y \biggr] \tag{3.32} \]

上式を y に関して0からY まで積分すると

\begin{align*} \int_{0}^{Y} \bigl( T_{Am} -T_B \bigr) \cdot dy & = Y \cdot \bigl( T_{Am} -T_B \bigr) \\ & =- \frac{G_B \cdot c_{pB}}{K \cdot X} \cdot \bigl(T_{Am} -T_{B1} \bigr) \cdot \biggl[ \exp \biggl(- \frac{K \cdot X \cdot Y}{G_B \cdot c_{pB}} \biggr) - 1 \biggr] \tag{3.33} \end{align*}

ここで、\(\displaystyle \frac{K \cdot X \cdot Y}{ G_B \cdot c_{pB}} =NTU_B \) を用いて整理すると次式を得る。

\[ T_{Am} =T_{Bm}- \frac{1} {NTU_B} \cdot \bigl(T_{Am} -T_{B1} \bigr) \cdot \bigl[ \exp \bigl(- NTU_B\bigr) - 1 \bigr] \tag{3.34} \]

同様にして、

\[ T_{Bm} =T_{Am}- \frac{1} {NTU_A} \cdot \bigl(T_{Bm} -T_{A1} \bigr) \cdot \bigl[ \exp \bigl(- NTU_A\bigr) - 1 \bigr] \tag{3.35} \]

式(3.33)、(3.34)からT_Am 、T_Bm を求め、式(3.2)に代入し整理すると次式となる。

\[ Q = \frac{ K \cdot X \cdot Y \cdot \bigl( T_{A1}- T_{B1} \bigr) }{ NTU_A \big/ \big[ 1- \exp \bigl(- NTU_A \bigr) \big]+NTU_B \big/ \bigl[ 1- \exp \bigl(- NTU_B \bigr) \bigr] -1} \tag{3.36} \]

一方、流体Aの温度変化から

\[ Q = G_A \cdot c_{pA} \cdot \bigl( T_{A1}- T_{A2} \bigr) \tag{3.37} \]

したがって、NTU_B=NTU_A/R を用いて整理すると温度効率は次式で表される。

\begin{align*} \epsilon_A & = \frac{T_{A1}-T_{A2}}{T_{A1}-T_{B1}} \\ & = \frac{ 1}{ 1 \big/ \big[ 1- \exp \bigl(- NTU_A \bigr) \big]+1 \big/ \big\{ R \cdot \bigl[ 1- \exp \bigl(- NTU_A/R \bigr) \bigr] \big\}-1 \big/ NTU_A } \tag{3.38} \end{align*}

\[\epsilon_B = \frac{T_{B2}-T_{B1}}{T_{A1}-T_{B1}} = R \cdot \epsilon _A \tag{3.39} \]

(b)一方の流体のみ混合する場合

　両流体が混合する場合と同様に、流体A、Bが長さX ,高さY の隔板を介して熱移動する場合を考える。ここで、流体Aは流れの断面方向に混合、流体Bは流れの断面方向に混合しないとする。

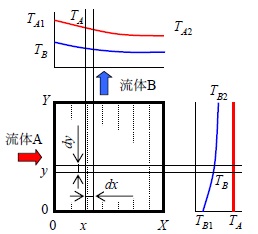
図 3.5　一方の流体のみ混合する場合の熱伝達

x 、y の位置から微小面積dx・dy での交換熱量は次式で表される。

\[dQ=K \cdot \bigl( T_A -T_B \bigr) \cdot dx \cdot dy \tag{3.40} \]

流体Bは非混合であり、温度変化から次式を得る。

\[dQ=G_B \cdot c_{pB} \cdot dT_B \cdot \frac{dx}{X} \tag{3.41} \]

したがって次式を得る。

\[\frac{dT_B}{dy}=\frac{K \cdot X}{G_B \cdot c_{pB}} \cdot \bigl( T_A - T_B \bigr) \tag{3.42} \]

T_A はx のみの関数であるために、上式をy=0 でT_B=T_B₁の境界条件から解き、次式を得る。

\[ T_A - T_B=\bigl( T_A - T_{B1} \bigr) \cdot \exp \biggl( - \frac{K \cdot X \cdot y}{G_B \cdot c_{pB}} \biggr) \tag{3.43} \]

したがって、T_B₂ は、\( NTU_B = K \cdot X \cdot Y \big/ \bigl( G_B \cdot c_{pB} \bigr) \)　とおけば次式となる。

\[ T_{B2}=T_A - \bigl( T_A - T_{B1} \bigr) \cdot \exp \bigl( - NTU_B \bigr) \tag{3.44} \]

微小面積Y・dx での流体A,Bの熱収支から次式を得る。

\begin{align*} -G_A \cdot c_{pA} \cdot dT & =G_B \cdot c_{pB} \cdot \frac{dx}{X} \bigl( T_{B2} - T_{B1} \bigr) \\ & =G_B \cdot c_{pB} \cdot \frac{dx}{X} \cdot \bigl( T_{A} - T_{B1} \bigr) \cdot \bigl( 1 - \exp (NTU_B) \bigr) \tag{3.45} \end{align*}

式（）を代入して整理すると次式が得られる。

\[ \frac{dT_A}{dx}= -R\cdot \frac{1}{X} \cdot \bigl( T_{A} - T_{B1} \bigr) \cdot \exp \bigl[ 1 - \exp (-NTU_B) \bigr] \tag{3.46} \]

上式をx=0 でT_A=T_A₁の境界条件から解き、次式を得る。

\[ T_A - T_{B1}=\bigl( T_{A1} - T_{B1} \bigr) \cdot \exp \biggl\{ -R\cdot \frac{x}{X} \cdot \bigl[ 1 - \exp (-NTU_B) \bigr] \biggr\} \tag{3.47} \]

したがって、面積X・Y での交換熱量は次式となる。

\begin{align*} Q & =K \cdot \int \int \bigl( T_{A} - T_{B} \bigr) \cdot dx \cdot dy \\ & =G_A \cdot c_{pA} \cdot \bigl( T_{A1} - T_{B1} \bigr) \cdot \bigl[ 1 - \exp \bigl\{ -R \cdot \bigl[ 1- \exp \bigl( -NTU_B \bigr) \big\}\bigr] \tag{3.48} \end{align*}

一方、流体Aの温度変化から交換熱量は次式で表される。

\[ Q=G_A \cdot c_{pA} \cdot \bigl( T_{A1} - T_{A2} \bigr) \tag{3.49} \]

したがって、温度効率は次式となる。

\[\epsilon_A = \frac{T_{A1}-T_{A2}}{T_{A1}-T_{B1}} = 1 - \exp \bigl[ -R \cdot \bigl\{ 1- \exp \bigl( -NTU_B \bigr) \bigr\} \bigr] \tag{3.50} \]

\[\epsilon_B= \frac{T_{B2}-T_{B1}}{T_{A1}-T_{B1}} = \frac{\epsilon_A}{R} \tag{3.51} \]